进制转换

基本知识

生活中最常见的是十进制运算,但在编程领域,与机器进行沟通的通常都是二进制的数据(要么0要么1)。

先来看十进制：

$$567=5×10^2+6×10^1+7×10^0$$

所以其公式可以表示为

$${Value} = d_n \times b^n + d_{n-1} \times b^{n-1} + \dots + d_1 \times b^1 + d_0 \times b^0 \ \ \ \\ ----\\ 0.0.1$$

公式中

• n表示第n位(从地位往高位索引)
• $d_n$表示第n位的系数
• b表示进制单位(如2进制，8进制，10进制)

上述公式还可以简化成

$$\text{Value} = \sum_{i}^{n} d_i \times b^i \\ ----\\ 0.0.2$$

公式说明:

1. i是整数(包含负数),负数的情况说明是有小数位

2. n表示最高位的指数

   $$eg. \ \ 567 \ \ \ 最高位的指数为 \ \ 2 \ \ 即 \ \ 10^2$$

---

eg.567.765 套入公式来看如下

$$567.765 = 5 \times 10^2 + 6 \times 10^1 + 7 \times 10^0 + 7 \times 10^{-1} + 6 \times 10^{-2} + 5 \times 10^{-3}$$

---

根据上述公式,来分析一下二进制数据

$$101101 = 1 × 2^5 + 0 × 2^4 + 1 × 2^3 + 1 × 2^2 + 0 × 2^1 + 1 × 2^0$$

综上101101=45

不同进制的转换均遵守上述公式

---

不同进制的数据可以通过不同的符号表示。下面是常见进制的表示方式：

1. 二进制（Base-2）：通常用前缀 0b 或 b 表示。例如，101101 可以写作 0b101101。

2. 八进制（Base-8）：通常用前缀 0o 或 o 表示。例如，55 可以写作 0o55。

3. 十进制（Base-10）：通常不需要前缀，直接写数字。例如，45。

4. 十六进制（Base-16）：通常用前缀 0x 表示。例如，2D 可以写作 0x2D。

---

进制转换

首先来了解一下小学三年级的基本概念

余数必须小于除数

$$被除数(Dividend) ÷ 除数(Divisor) = 商(quotient)...余数(Remainder)$$

5 ÷ 3 = 1 … 2

• 被除数（Dividend）：5
• 除数（Divisor）：3
• 商（Quotient）：1
• 余数（Remainder）：2

1 ÷ 2 = 0 … 1

---

我们仍旧以567数据为例，看看为什么其十进制的表示方法是567,以公式0.0.1分析:

$$567 = 5×10^2+6×10^1+7×10^0 \\ ----\\ 567÷10 = 56...7 = (5×10^2 + 6×10^1) ... 7×10^0 \ \ \ \ 即d_0 = 7 \\ 取其商继续整除10\\ ----\\ 56÷10 = 5...6 = 5×10^1 + 6×10^0 \ \ \ \ 即d_1 = 6 \\ 取其商继续整除10\\ ----\\ 5÷10 = 0...5 = 5 ×10^0 \ \ \ \ 即d_2 = 5 \\ ----\\ \\ 综上可知,其10进制的的表示方法即\\ d_2d_1d_0 = 567$$

那么567以二进制表示方式该怎么表示呢？同样的除以 2，取其余数

$$567 ÷ 2 = 283 ... 1 \ \ \ \ 即d_0 = 1 \\ 283 ÷ 2 = 141 ... 1 \ \ \ \ 即d_1 = 1 \\ 141 ÷ 2 = 70 ... 1 \ \ \ \ \ 即d_2 = 1 \\ 70 ÷ 2 = 35 ... 0 \ \ \ \ 即d_3 = 0 \\ 35 ÷ 2 = 17 ... 1 \ \ \ \ 即d_4 = 1 \\ 17 ÷ 2 = 8 ... 1 \ \ \ \ 即 d_5 = 1 \\ 8 ÷ 2 = 4 ... 0 \ \ \ \ 即 d_6 = 0 \\ 4 ÷ 2 = 2 ... 0 \ \ \ \ 即 d_7 = 0 \\ 2 ÷ 2 = 1 ... 0 \ \ \ \ 即 d_8 = 0 \\ 1 ÷ 2 = 0 ... 1 \ \ \ \ 即 d_9 = 1 \\ ---\\ 所以其二进制的数据为\\ d_9d_8d_7d_6d_5d_4d_3d_2d_1d_0 = 10 \ 0011 \ 0111$$

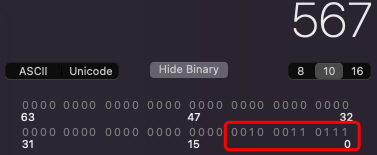
根据上面的分析,进制的转换就比较简单了。

• 连续的三个 二进制的 bit 位就表示一个 八 进制的数据
• 连续的四个 二进制的 bit 位就表示一个 十六 进制的数据

接着以567为例，我们通过科学学计算器来分别看一下 8进制和16进制的数据

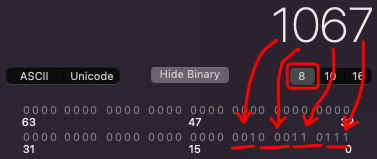
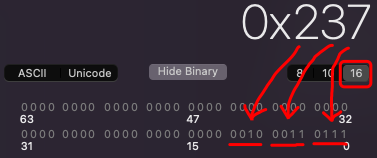
所以:

$$(567)_{10} = (1000110111)_{2} = (1067)_{8} = (0×237)_{16}$$

右下位置角标表示对应的进制,内部括号可以省略。

---

综上只要理解了公式0.0.1,万变不离其宗,根据其二进制的数字,便可以轻松实现不同进制的转换;